java递推算法-设计递归算法的基本原则、基本情形、解决、合并

递归算法

所谓递归，就是指函数用自己来定义，通俗来讲就是函数调用自身的函数方法。递归算法式采用了 分治法的思想。分治法主要分为三个步骤，分解、解决、合并。

严格来讲，每一个递归式都可以用循环结构来替代java递推算法，那为什么我们要写递归式呢？我们写递归式是为了让代码看起来更简洁清晰。 设计递归算法的基本原则

基本情形：递归算法应该有一个基本情形，当程序运行至某些情况时，会有递归出口，它们不需要递归来解决问题。

不断逼近：将需要进行递归求解的情形不断通过递归的基本情形。

递归算法在java中是如何运行的

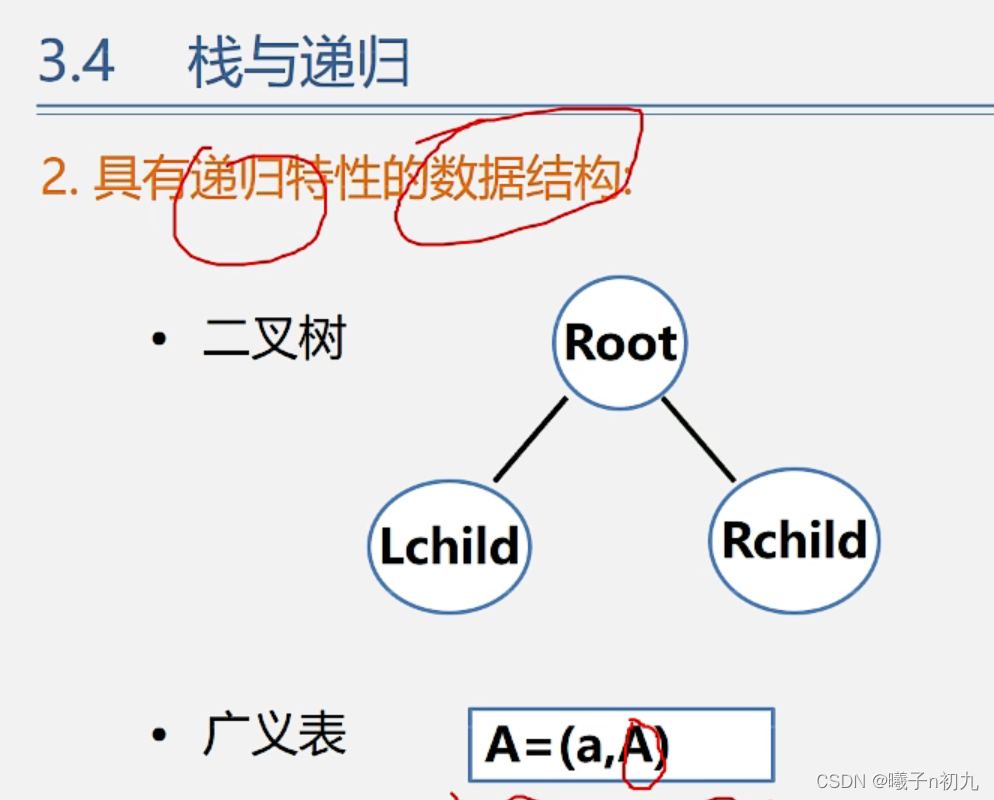
java在运行递归程序式，会采用栈这种数据结构进行处理的。java运行递归程序时，会自动开辟一块空间用于创立栈空间。递归算法基本情形也就是栈的顶部，当程序运行至基本情形时，这时栈中算有的情形会依次执行栈内的。

每个递归方法中的基本变量都是独立的，引用变量是相同的，都指向同一块地址内存！

几种递归算法 通过递归来求解最大子数组

public static int max3(int a, int b, int c){
        if(a >= b && a >= c) return a;
        else if(b >= a && b >= c) return b;
        else  return c;
    }
    public static int maxSumRec(int[]  a, int left, int right){
    	//基本情形
        if( left == right){
            return a[left];
        }
        int center = (left + right) / 2;
        //开始递归
        int maxLeftSum = maxSumRec(a, left, center);
        int maxRightSum = maxSumRec(a, center + 1, right);
        int maxLeftBorderSum = 0, leftBoderSum = 0;
        for (int i = center; i >= left; i--){
            leftBoderSum += a[i];
            if(leftBoderSum > maxLeftBorderSum){
                maxLeftBorderSum = leftBoderSum;
            }
        }
        int maxRightBorderSum = 0, rightBorderSum = 0;
        for(int i = center + 1; i <= right; i++){
            rightBorderSum += a[i];
            if(rightBorderSum > maxRightBorderSum)
                maxRightBorderSum = rightBorderSum;
        }
        return max3(maxLeftSum, maxRightSum, maxLeftBorderSum + maxRightBorderSum);
    }

该算法通过将原问题分解成求子数组的左边最大子数组、右边最大子数组以及跨越了中间三种情况。

将左边最大子数组、右边最大子数组不断递归java递推算法，将数组缩小至只有一个元素的基本情形，再不断求解。

归并排序

public static void merge(int a[], int p, int q, int r) {
        int n1 = q - p + 1;
        int n2 = r - q;
        int[] L = new int[n1+1];
        int[] R = new int[n2+1];
        for(int i = 0;i < n1; i++){
            L[i] = a[p+i];
        }
        for(int i = 0;i < n2; i++){
            R[i] = a[q+i+1];
        }
        L[n1] = Integer.MAX_VALUE;
        R[n2] = Integer.MAX_VALUE;
        int i = 0;
        int j = 0;
        for(int k = p; k <= r;k++){
            if(L[i] <= R[j]){
                a[k] = L[i];
                i++;
            }
            else{
                a[k] = R[j];
                j++;
            }
        }
    }
    public static void mergeSort(int[] a,int p, int r){
        if(p < r){
            int q = (p+r)/2;
            mergeSort(a,p,q);
            mergeSort(a,q+1,r);
            merge(a,p,q,r);
        }
    }

归并排序也是通过数组不断缩小，然后再对其进行排序的算法，该算法的基本情形同意也是只有一个元素，也就是p等于r的时候。