二叉树 python-树,森林与二叉树的转换
Python二叉树第一次(新手在几秒钟内理解!
更新时间:2022-05-27 11:22:10 作者:汉阳
二叉树是
一个简单的树形结构,每个节点的分支节点数有0、1或2个,下面文章主要介绍一下Python二叉树的相关信息,这篇文章很好理解,新手也秒级明白,需要的朋友可以参考
内容
树
树是一组有限的 n(n≥0) 个节点。
在任何树中:
(1)只有一个特定的节点称为根;
(2)当n>1时,剩余节点可分为m(m>0)为不相交有限集T1、T2,...,Tm;
这些集合中的每一个本身都是一棵树,称为根子树。
树:
--------------------
高度=4 列维斯=5 根
度数=3 大小=26 ↙____
__ 节点级别 1/
/ \ ↙26______ 2 ____
9__ ←- 儿童2级/ \ \ /
/ / \___0 19 _3___
6 ___21 15 3级/ / / \
/ \ /
7 _16 _24 _8 10 4 23 级别4/ \ / / /
\ / \ /5
11 28 13 1 27 29 18 22 等级5↑
↑↑___↑____
___↑...叶子左子 右子
术语节点
:包含一个数据元素和几个指向其子树的分支,也称为“节点”根
:树和子树的“根”度数
:节点拥有的子树数称为节点度数;树的度数是树内每个节点的度数的最大值
分支节点:度数不是 0 的节点
叶:没有子树的节点,即它的度数为 0(叶)。
子节点:根节点的子
树称为该节点的子节点父节点
:对应子节点上方的级别节点称为节点的父节点同级节点
:同一父节点的子节点,称为彼此兄弟(同级)。节点
的祖先:分支上从根到节点的所有节点节点
的后代:子树中根植于节点的所有节点
层:从根开始,根是
第一层,根的子层是第二层...(级别)深度
:树中节点的最大层数,称为树的深度或高度
森林
:是许多不相交的树(森林)的集合。无序树
:树中任何节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树
有序树:有一个树
中任何节点的子节点之间的顺序关系,称为有序树
最大的树(
最小树):每个节点的值大于(小于)或等于其子节点的值(如果有)的树。
二叉树
二叉树是一种特殊的有序树结构。
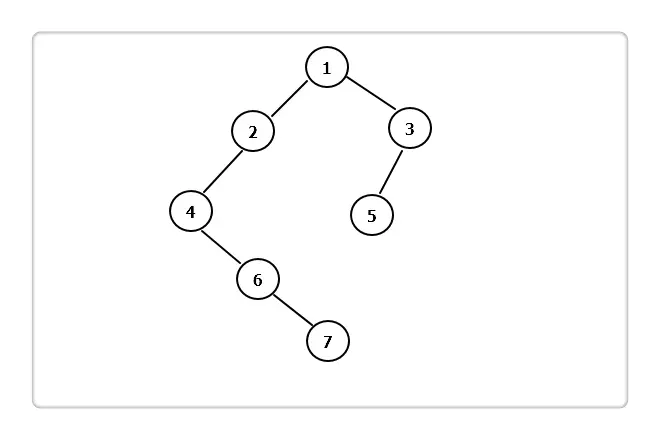
特征:
(1)每个节点最多有两个子树;
(2)二叉树的子树有左右分界线;(
3)子树的顺序不能任意颠倒(有序树)。
自然界:(1)
二叉树第i层最多2^(i-1)节点(i>=1);(
2)深度为k的二叉树最多有2^k-1个节点(k>=1);
(3)对于任何二叉树,如果它的叶节点数为N0,度数为2的节点数为N2,则N0=N2+1。特殊二叉树
全二叉树:所有
层都有达到其最大数量的节点,除叶子之外的所有节点都有两个子节点,所有叶子都在底层 (k) 中,数量为 2^(k- 1)。也就是说,深度 k 和 2^k - 1 个节点(叶子“生长”到最后一层),或完美二叉树______
12_______
/ \__3__ __
5__/ \
/ \_
7 6 _9 11/ \ / \
/ \ / \
13 8 1 4 10 2 0 14
完整的二叉树:
如果删除底层的所有叶子,就是一个完整的二叉树,即除最后一层外二叉树 python,每层节点数达到最大数量,即深度为k的节点数在左闭右[2^(k-1)+1,2^k-1]区间内。 (完整的二叉树)______
__3______
/ \___
11___ __4__/ \
/ \
14 7 9 13/ \ /
\ /
2 5 8 6 1
完整的二叉树属性:
1. 具有 N 个节点的完整二叉树的深度为 [log2 N]+1,其中 [x] 是高斯函数,截断和舍入。
2. 如果具有 n 个节点的完整二叉树的节点按顺序编号(从第一层到最后一层,每层从左到右),那么对于任何节点,都有:
(1)如果i = 1,则节点i是二叉树的根,没有父项;如果为 i>1,则其父节点为 [i/2];
(2)如果为2i>n,则节点i没有左子节点;否则,其左子节点是节点 2i;
(3)如果2i+1>n,节点i没有右子节点;否则,其右子节点是节点 2i+1。
其他特殊二叉树
对二叉树进行排序二叉搜索树
,也称为二叉搜索树或有序二叉树
平衡二叉树左右子树
之间高度差不超过1的二叉树,并且必须有:它的左右子树也是自平衡二叉搜索树
退化的树木退化树是每个节点只有一个子节点的树,
子节点是左树或右树,或者病树
斜二叉树
一种特殊的退化树,其中所有节点只有左子节点或右
子节点,分别称为左斜二叉树和右斜二叉树,函数基本降级为与链表相同
霍夫曼树
二叉树
具有最短加权路径的路径称为霍夫曼树或最优二叉树
B树
针对读取和写入操作优化的自平衡二叉树查找,通过两个额外的子树保持数据组织
堆
堆二叉
堆是一个完整的二叉树二叉树 python,除了最低的叶节点之外,它被填充;而且,最低的叶节点从左到右是连续的,不能有间隙。最大的堆(最小的堆)是最大(最小的)完整二叉树。
二叉树的遍历
它是指如何通过一定的搜索路径对树中的每个节点进行巡查,使每个节点访问一次且只能访问一次。
常见的遍历方法有:一阶遍历、中阶遍历、后阶遍历
、层序遍历;这通常是使用递归算法实现的。
以一个完整的二叉树为例:_______1______
__
/ \__2__ _
__3___/ \
/ \
4 5 _6 _7/ \ / \
/ \ / \
8 9 10 11 12 13 14 15
先遍历
如果二叉树为空,则为空操作;
否则,(1) 访问根节点;(2)先遍历左子树;(3) 先遍历右子树。
遍历结果: 1 [2 [4 8 9] [5 10 11]] [3 [6 12 13] [7 14 15] “根左右”

中阶遍历
如果二叉树为空,则为空操作;
否则,(1)以中间顺序遍历左侧子树;(2)访问根节点;(3)按中间顺序遍历右子树。
迭代结果: [[8 4 9] 2 [10 5 11]] 1 [[12 6 13] 3 [14 7 15]] “左根右”

后序遍历
如果二叉树为空,则为空操作;
否则,(1) 遍历后序中的左子树;(2)右子树的后序遍历;(3) 访问根节点。
遍历结果: [[8 9 4] [10 11 5] 2] [[12 13 6] [14 15 7] 3]1 “左右根”

层序遍历
如果二叉树为空,则为空操作;否则,访问从上到下、从左到右是分层的。
遍历结果: 1 [2 3] [4 5 6 7] [8 9 10 11 12 13 14 15]。

非完整二叉树的遍历结果:________
1______
/ \__2___
___3/ \
/ \
4 _5 6 7\ / \
/ \
9 10 11 12 15
序列: 1 [2 [4 ' 9] [5 10 11]] [3 [6 12 '] [7 ' 15]]。
中间顺序: [' 4 9] 2 [10 5 11] 1 [12 6 '] 3 [' 7 15]。
后奏: [['9 4] [10 11 5] 2] [[12 ' 6] [' 15 7] 3] 1
层序: 1 [2 3] [4 5 6 7] [' 9 10 11 12 ' ' 15]。
注意:结果中的 ' 仅标记相对于完整二叉树缺少的子节点,不显示实际结果。
Python 实现二叉树
在 Python 中简单实现以下二叉树遍历函数,并列出层数和所有叶子:
______一个______
/ \
__B__ __C__/ \
/ \

德·英·/ \
/ \ \ \
H I J K L M
代码如下:
class Node():
def __init__(self, data=None, left=None, right=None):
self.data = data
self.left = left
self.right = right
def Preorder(self):
if self.data is not None:
print(self.data, end=' ')
if self.left is not None:
self.left.Preorder()
if self.right is not None:
self.right.Preorder()
def Inorder(self):
if self.left is not None:
self.left.Inorder()
if self.data is not None:
print(self.data, end=' ')
if self.right is not None:
self.right.Inorder()
def Postorder(self):
if self.left is not None:
self.left.Postorder()
if self.right is not None:
self.right.Postorder()
if self.data is not None:
print(self.data, end=' ')
def Height(self):
if self.data is None:
return 0
elif not any([self.left, self.right]):
return 1
elif all([not self.left, self.right]):
return self.right.Height()+1
elif all([self.left, not self.right]):
return self.left.Height()+1
else:
return max(self.left.Height(), self.right.Height())+1
def Leaves(self):
if self.data is None:
return None
elif not any([self.left, self.right]):
print(self.data, end=' ')
elif all([not self.left, self.right]):
self.right.Leaves()
elif all([self.left, not self.right]):
self.left.Leaves()
else:
self.left.Leaves()
self.right.Leaves()
bt = Node('A')
bt.left = Node('B')
bt.right = Node('C')
bt.left.left = Node('D')
bt.left.right = Node('E')
bt.right.left = Node('F')
bt.right.right = Node('G')
bt.left.left.left = Node('H')
bt.left.left.right = Node('I')
bt.left.right.left = Node('J')
bt.left.right.right = Node('K')
bt.right.left.right = Node('L')
bt.right.right.right = Node('M')
print('Perorder:')
bt.Preorder()
print('\nInorder:')
bt.Inorder()
print('\nPostorder:')
bt.Postorder()
print('\nTree Height:\n',bt.Height())
print('\nLeaves:')
bt.Leaves()
运行结果:
顺序:
A B D H I E J K C F L G M
序:
H D I B J E K A F L C G M
后序:
H I D J K E B L F M G C A
树高:# 其实是层数,相当于建筑物的高度和底层的高度从 0
四
叶:
H I J K L M
要实现二叉树的所有全部功能,代码必须庞大。最好找到一个好的第三方库!!!
二叉树第三方库二进制树使用环境和安装
要求: Python 3.6+
安装:
>点安装二进制树
对于康达用户:
>conda install binarytree -c conda-forge
简单实例
二进制树。节点() 二叉树节点
from binarytree import Node root = Node(1) root.left = Node(2) root.right = Node(3) root.left.right = Node(4) print(root) # 或者: root.pprint() # # __1 # / \ # 2 3 # \ # 4 #
binarytree.tree() random binary tree
from binarytree import tree bt = tree(is_perfect=True) bt.pprint() # # _______14______ # / \ # ___13__ __8__ # / \ / \ # _9 0 6 3 # / \ / \ / \ / \ # 10 12 5 7 4 2 1 11 #
下一个准备练习这个第三方库二进制树!
有关本文的续篇,请单击以下链接:
-
二叉树的初步探索,第三方库二元树
总结
至此,这篇关于Python二叉树的文章初识
这里介绍一下,更多相关的Python二叉树初识内容,请搜索脚本屋之前的文章或者继续浏览以下相关文章,希望大家以后能多支持脚本屋!


 上一篇
上一篇 








