动态规划 背包 java-动态规划算法背包问题

文章目录

动态规划算法

动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中动态规划 背包 java，可能会有许多可行解。每一个解都对应于一个值动态规划 背包 java，我们希望找到具有最优值的解。动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。与分治法不同的是，适合于用动态规划求解的问题，经分解得到子问题往往不是互相独立的。若用分治法来解这类问题，则分解得到的子问题数目太多，有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，这样就可以避免大量的重复计算，节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样，但它们具有相同的填表格式。

案例：01背包问题

01背包是一个背包中不能重复放置同一件物品。完全背包是一个背包可以放置同一件物品。

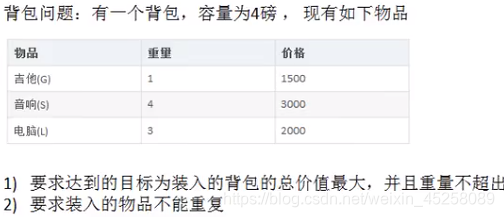
. 思路分析

. 代码实现

public class DynamicProgramming {
    public static void main(String[] args) {
        int p[] = {1500,3000,2000}; // 物品价格
        int w[] = {1,4,3}; //物品重量
        int packWeight = 4;
        int v[][] = new int[w.length+1][packWeight+1]; // 动态规划价格表
        int putIn[][] = new int[w.length+1][packWeight+1]; // 用于记录物品是否被放入，放入为1
        // 第一行，第一列都为0
        for (int i = 0; i < v[0].length; i++) {
            v[0][i] = 0;
        }
        for (int i = 0; i < v.length; i++) {
            v[i][0] = 0;
        }
        // 从索引为1的行开始，从索引为1的列开始
        for (int i = 1; i < v.length; i++) {
            for (int j = 1; j < v[0].length; j++) {
                // 如果第i-1个物品的重量大于此时背包重量j，那么这个物品就不能放入背包中
                // 表就应该填入上一个满足要求的价格
                if (w[i-1] > j){
                    v[i][j] = v[i-1][j];
                }
                // 如果第i-1个物品的重量小于或等于此时背包的重量j，那么就判断这个物品的价格是否
                // 大于上一个满足要求的价格，如果小于就填入将上一个满足要求的价格，否则就填入该
                // 物品的价格加上剩余重量满足的最大价格
                if (w[i-1] <= j){
                    //v[i][j] = Math.max(v[i-1][j], v[i-1][j-w[i-1]]+p[i-1]);
                    if (v[i-1][j] < v[i-1][j-w[i-1]]+p[i-1]){
                        v[i][j] = v[i-1][j-w[i-1]]+p[i-1];
                        putIn[i][j] = 1; // 记录物品被放入
                    }else {
                        v[i][j] = v[i-1][j];
                    }
                }
            }
        }
        // 输出最大价格放入的物品
        int i = putIn.length-1;
        int j = putIn[0].length-1;
        int Price = 0;
        while (i>0 && j>0){
            if (putIn[i][j] == 1){
                System.out.println("第"+i+"个物品放入背包中");
                Price += p[i-1]; // 求价格总和
                j -= w[i-1];
                // 每输出一个商品，就减去该商品的重量，求出书包剩下的重量，对应价格表中的索引
            }
            i--;
        }
        System.out.println("最大价格: "+Price+"元");
//        for (int[] ints : v) {
//            System.out.println(Arrays.toString(ints));
//        }
//
//        for (int[] ints : putIn) {
//            System.out.println(Arrays.toString(ints));
//        }
    }
}

结果：

第3个物品放入背包中
第1个物品放入背包中
最大价格: 3500元