01背包问题回溯法java-0 1背包问题 回溯

3.2 动态规划算法

介绍：

动态规划算法经典问题—背包问题

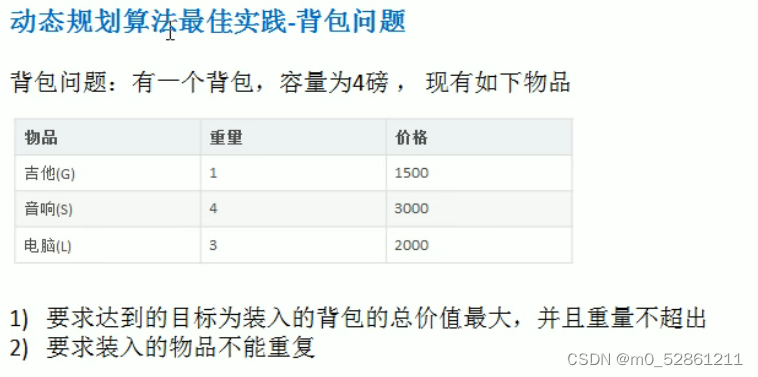
思路：

为什么背包最大容量C已经给定01背包问题回溯法java，代表背包容量的J还要设置为可变的呢？

​ 因为我们是在进行动态规划，v[i][j]代表容量为J的背包存放i个物品可以获取的最大价值，是在背包容量为j时的最优解。当J增长时01背包问题回溯法java，在计算新的局部最优解是需要考虑J更小时的其他局部最优解。比如在J=4时，我们需要考虑J=2、J=1时的局部最优解，从而计算得到J=4时的全部最优解

在每一次添加新物品到容量为 J 的背包中，需要进行以下流程判断

使用一张图来方便理解

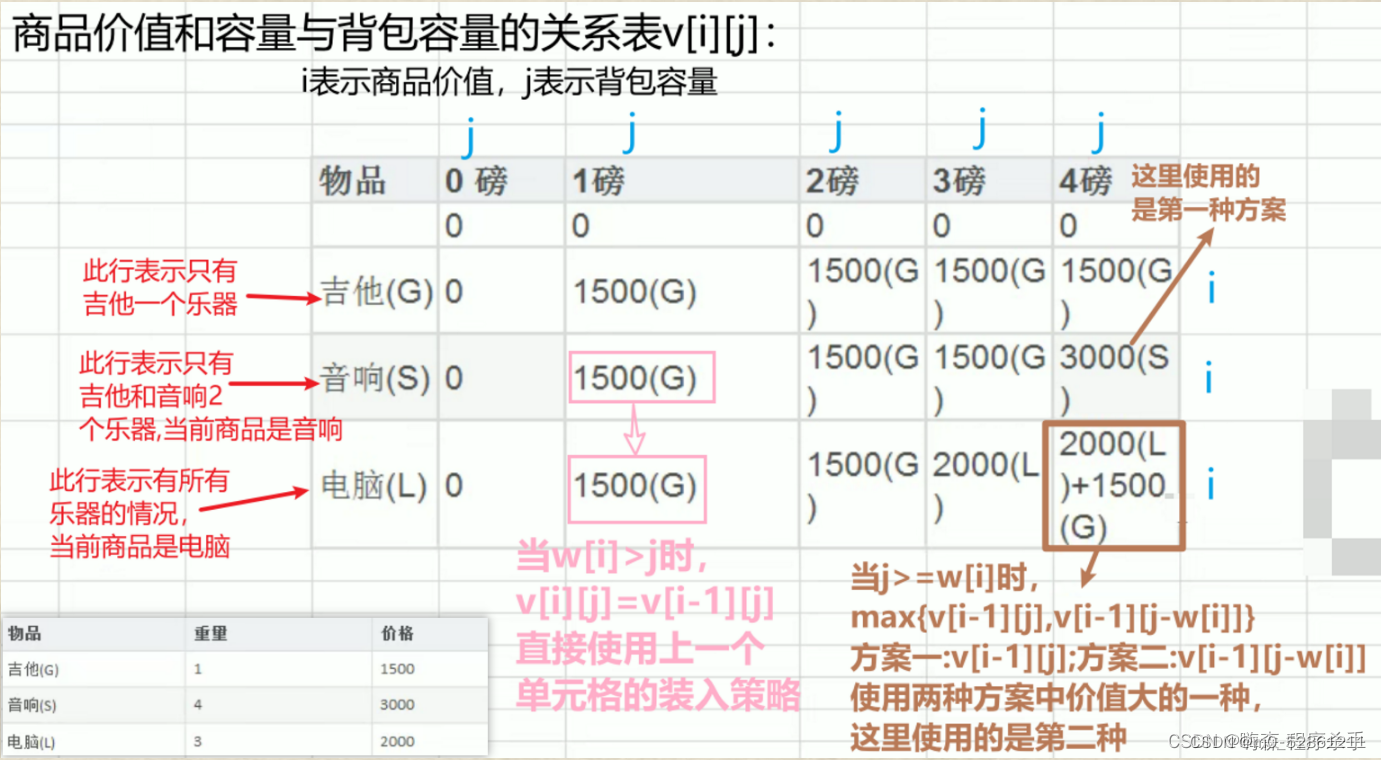
代码：

import java.util.Arrays;
public class knapsack {
    public static void main(String[] args) {
        int[] w = {1, 4, 3};//物品的重量
        int[] val = {1500, 3000, 2000};//物品的价值
        int m = 4;//背包的容量
        int n = val.length;//物品的个数
        //为了记录放入商品的情况，我们定义一个二维数组
        int[][] isPut = new int[n + 1][m + 1];
        //创建二维数组
        //v[i][j]：表示在前i个(种)物品中能够装入容量为j的背包中的最大价值
        int[][] v = new int[n + 1][m + 1];
        //初始化第一行和第一列【可有可无】
        for (int i = 0; i < v.length; i++) {//v.length:获取二维数组的行数
            v[i][0] = 0;//将第一列设置为0
        }
        //将第一行设置为0
        Arrays.fill(v[0], 0);
        // 因为前面初始化过第一行和第一列的数值固定为0，所以以下i和j下标从1开始
        for (int i = 1; i < v.length; i++) {
            for (int j = 1; j < v[0].length; j++) {
                // w[i] 需要从0开始
                if (w[i-1] > j) { // 添加物品重量大于背包容量大小
                    v[i][j] = v[i - 1][j];
                } else {
                    // 若将物品加入到背包内最大价值最大,将物品加入到背包内
                    if (v[i - 1][j] < (val[i - 1] + v[i - 1][j - w[i - 1]])) {
                        v[i][j] = val[i - 1] + v[i - 1][j - w[i - 1]];
                        // 若将新物品加入到背包内 在标记数组内标记
                        isPut[i][j] = 1;
                    } else { // 选择不将新物品加入到背包内
                        v[i][j] = v[i - 1][j];
                    }
                }
            }
        }
        //输出最后我们是放入的那些商品
        int i = isPut.length - 1;
        int j = isPut[0].length - 1;
        System.out.println("最大价值: "+v[i][j]);
        System.out.println("添加物品情况: ");
        // 从最后一个物品开始，判断在J容量下有没有加入对应物品
        //      1.没有加入就判断前一个物品在J容量下有没有加入背包。
        //      2.加入了,就判断剩余背包容量下J-W[i]下前一个物品有没有加入
        //      3.直到全部物品都检查过一遍后才停止
        while (i > 0 && j > 0) {//从加入的最后一个物品开始倒序查找
            if (isPut[i][j] == 1) {
                System.out.printf("第%d个商品放入背包\n", i);
                j -= w[i - 1];
            }
            i--;
        }
    }
}

输出结果：

最大价值: 3500
添加物品情况: 
第3个商品放入背包
第1个商品放入背包

参考博客：

详解：动态规划算法【Java实现】——背包问题_动态规划背包问题时间效率_嗨森-程序杀手的博客-CSDN博客