最长公共子序列java-java序列话部分字段
[问题] 找出双字符序列的最长公共字符子序列
问题描述:字符序列的子序列是指从给定的字符序列中随机(不一定连续)去掉几个字符(也可能没有)形成的字符序列。 设给定的字符序列 X="x0,x1,...,xm-1",序列 Y="y0,y1,...,yk-1" 是 X 的子序列,存在严格递增的下标X 的序列,对于所有 j=0, 1, ..., k-1最长公共子序列java,令 xij=yj。 例如,X="ABCBDAB", Y="BCDB" 是 X 的子序列。
考虑最长公共子序列问题如何分解为子问题,设A = "a0, a1, ..., am-1", B = "b0, b1, ..., bm-1", Z = "z0 , z1, ... , zk-1" 是它们的最长公共子序列。 不难证明以下性质:
(1) 若am-1=bn-1,则zk-1=am-1=bn-1,“z0,z1,...,zk-2”为“a0,a1,...,am -2”和“b0, b1, ..., bn-2”的最长公共子序列;
(2) 如果am-1!=bn-1, 那么如果zk-1!=am-1, 意味着“z0, z1, ..., zk-1”是“a0, a1, ..., am- 2”和“b0, b1, ..., bn-1 的最长公共子序列”;
(3) 如果am-1!=bn-1, 那么如果zk-1!=bn-1, 意味着“z0, z1, ..., zk-1”是“a0, a1, ..., am- 1”和“b0, b1, ..., bn-2 的最长公共子序列”。
这样最长公共子序列java,在寻找A和B的公共子序列时,如果am-1=bn-1,则进一步求解一个子问题,找到“a0,a1,...,am-2”和“b0, b1, ..., a longest common subsequence of bm-2”;如果am-1!=bn-1,则需要求解两个子问题,找出“a0, a1, ..., am-2”和“b0, b1, ..., bn-1 的最长公共子序列”,求“a0, a1, ..., am-1” 和 “b0, b1, ..., bn-2” 的最长公共子序列,然后取两个中较长的一个就是A和B的最长公共子序列。
解决:
引入一个二维数组c[][],用c[i][j]记录X[i]和Y[j]的LCS长度,b[i][j]记录c[ i][j]是得到哪个子问题的值,来决定搜索的方向。
我们自下而上进行递归计算,然后在计算c[i,j]、c[i-1][j-1]、c[i-1][j]和c[i][j-1]之前已被计算。 这时候我们可以根据X[i] = Y[j]或者X[i] != Y[j]来计算c[i][j]。
问题的递归公式写为:
回溯输出最长公共子序列的过程:
算法分析:
由于每次调用至少向上或向左移动一步(或同时向上和向左移动),所以最多(m + n)次调用会遇到i = 0或j = 0的情况,并开始返回此时。 返回时,方向与递归调用的方向相反,步数相同,所以算法的时间复杂度为Θ(m + n)。
伪代码说:
for x = 0 to n do
for y = 0 to m do
if (x == 0 || y == 0) then
LCS(x, y) = 0
else if (Ax == By) then

LCS(x, y) = LCS(x - 1,y - 1) + 1
else
LCS(x, y) = ) max(LCS(x – 1, y) , LCS(x, y – 1))
endif
endfor
endfor
整个代码(能粘贴运行的那种):
package dp;
import java.util.Random;
//使用动态规划找出最长公共子序列
public class LCS {
public static void main(String[] args) {
//随机生成指定长度的字符串
int size = 20;
String x = generateRandomStr(size);
String y = generateRandomStr(size);
int m = x.length();
int n = y.length();
//创建二维数组,也就是填表的过程
int[][] c = new int[m+1][n+1];
//初始化二维数组
for (int i = 0; i < m+1; i++) {
c[i][0] = 0;
}
for (int i = 0; i < n+1; i++) {
c[0][i] = 0;
}
//实现公式逻辑
int[][] path = new int[m+1][n+1];//记录通过哪个子问题解决的,也就是递推的路径
for (int i = 1; i < m+1; i++) {
for (int j = 1; j < n+1; j++) {
if(x.charAt(i-1) == y.charAt(j-1)){
c[i][j] = c[i-1][j-1] + 1;

}else if(c[i-1][j] >= c[i][j-1]){
c[i][j] = c[i-1][j];
path[i][j] = 1;
}else{
c[i][j] = c[i][j-1];
path[i][j] = -1;
}
}
}
//输出查看c
System.out.println("c:");
for (int i = 0; i < m+1; i++) {
for (int j = 0; j < n+1; j++) {
System.out.print(c[i][j]+"\t");
}
System.out.println();
}
//输出查看path
System.out.println("path:");
for (int i = 0; i < m+1; i++) {

for (int j = 0; j < n+1; j++) {
System.out.print(path[i][j]+"\t");
}
System.out.println();
}
System.out.printf("%s与%s的最长公共子序列为:\n",x,y);
PrintLCS(path,x,m,n);
}
public static String generateRandomStr(int length) {
String base = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
Random random = new Random();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < length; i++) {
int number = random.nextInt(base.length());
sb.append(base.charAt(number));
}
return sb.toString();
}
public static void PrintLCS(int[][]b,String x,int i,int j){
if(i == 0 || j == 0){
return;
}
if(b[i][j] == 0){
PrintLCS(b,x,i-1,j-1);
System.out.printf("%c",x.charAt(i-1));
}else if(b[i][j] == 1){
PrintLCS(b,x,i-1,j);
}else{
PrintLCS(b,x,i,j-1);
}
}
}
程序运行截图:
总结
程序一般分为两部分。 首先是二维数组c的构造,本质上就是问题划分的过程。 由此可见,动态规划的方法是将所有可能的子问题一一列出,并选择 计算最终的最优解是有用的,避免重复计算。最优解最终出现在数组的结尾
第二部分是如何输出最优解。 这是新建一个path[][]数组,记录使用了哪个子问题,并在遍历过程中输出。 背包问题与最长公共子序列问题有很多相似之处,需要总结和反思。


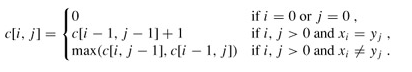


 上一篇
上一篇 








