java实现归并排序-归并排序算法C++实现（超详细解析！）

目录

归并排序的思想 归并排序算法C++实现（超详细解析！！！！）_c++归并排序_sunny-ll的博客-CSDN博客

简而言之，就是不断递归将序列平均分割，最后两两比较放入新序列中，再将新的序列复制给原来的序列。（已经排好序的部分不会重新排序）

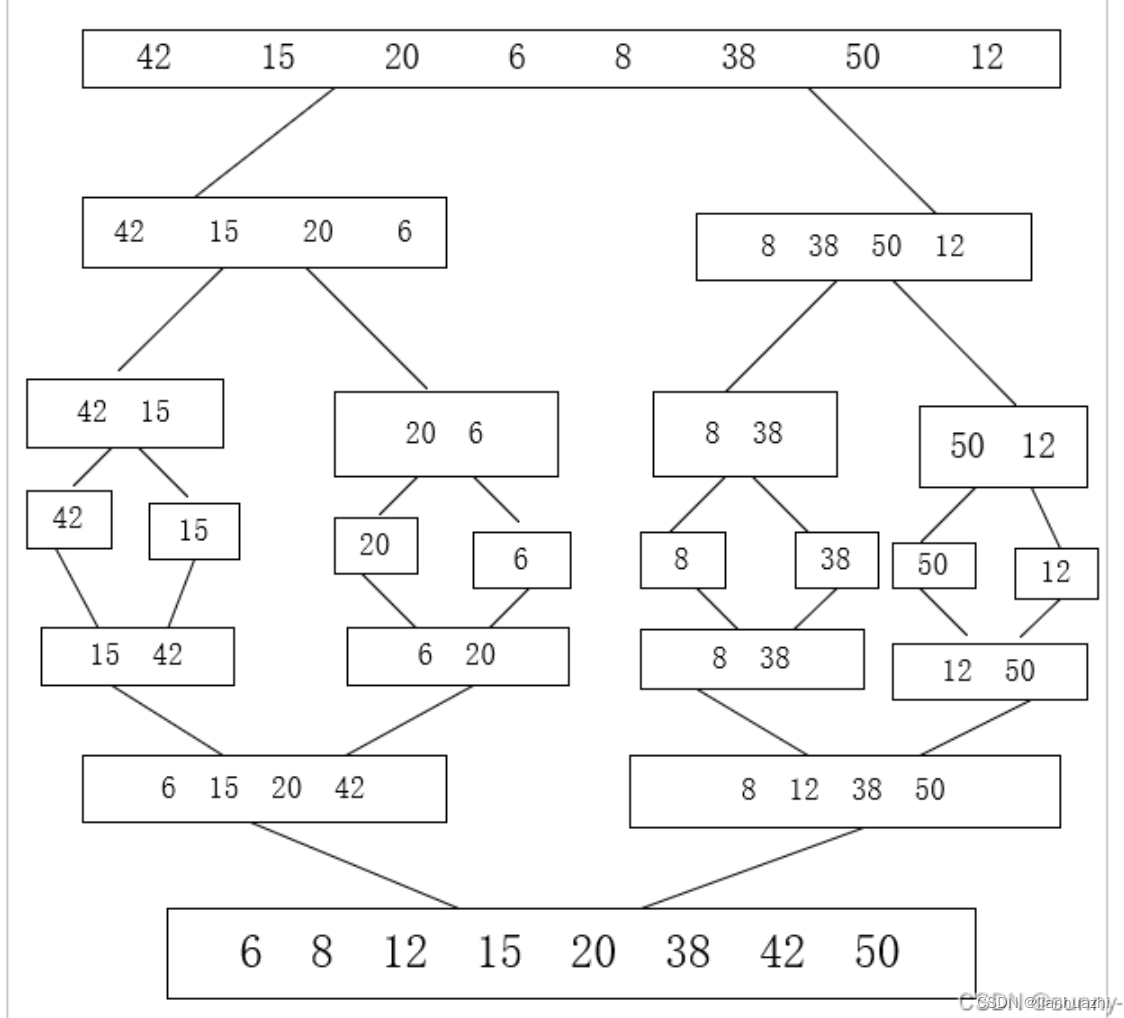
归并排序的实现

归并排序算法C++实现（超详细解析！！！！）_c++归并排序_sunny-ll的博客-CSDN博客

小和问题

归并排序算法C++实现（超详细解析！！！！）_c++归并排序_sunny-ll的博客-CSDN博客

就是找该数的左边比它本身小的和，转化为从前往后遍历，找到比该数大的个数的数量，最后结果就是答案=(每一个数)*（后面比该数大的数的个数）.

小和问题与归并排序的不同

将考虑在左边的数==右边的数时java实现归并排序，需要单独进行考虑，同时先把右边的数放进去。同时将该情况作为第一个if语句，另外的情况做else if 和else。

如果先放左边的数，那么右边如果还有相同的数，就会导致结果不正确。

例如：1233 1224

如果先放左边的2java实现归并排序，那么计算比它大是个数就会多一个。

小和问题的实现

【归并排序，小和问题，利用C++实现】_冲冲冲@chong的博客-CSDN博客

#include 
using namespace std;
void merge(int* a, int low, int mid, int hight)
{
	int* b = new int[hight - low + 1];  //用 new 申请一个辅助函数
	int p1 = low, p2 = mid + 1, k = 0;    // k为 b 数组的小标
	while (p1 <= mid && p2 <= hight)
	{
		if (a[p1] <= a[p2])
		{
			b[k++] = a[p1++];  //按从小到大存放在 b 数组里面
		}
		else
		{
			b[k++] = a[p2++];
		}
	}
	while (p1 <= mid)  // j 序列结束，将剩余的 i 序列补充在 b 数组中 
	{
		b[k++] = a[p1++];
	}
	while (p2 <= hight)// i 序列结束，将剩余的 j 序列补充在 b 数组中 
	{
		b[k++] = a[p2++];
	}
	k = 0;  //从小标为 0 开始传送
	for (int i = low; i <= hight; i++)
	{
		a[i] = b[k++];
	}
	delete[] b;
}
void mergesort(int* a, int n, int m) //指针如何传递？ 
{
	if (n < m)
	{
		int mid = (m + n) / 2;
		mergesort(a, n, mid);
		mergesort(a, mid + 1, m);
		merge(a, n, mid, m);
	}
}
int merge_min(int* a, int low, int mid, int hight)  //合并函数
{
	int* b = new int[hight - low + 1];  //用 new 申请一个辅助函数
	int i = low, j = mid + 1, k = 0;    // k为 b 数组的小标
	int res = 0;
	while (i <= mid && j <= hight)
	{
		if (a[i] == a[j])
		{
			b[k++] = a[j++];  //按从小到大存放在 b 数组里面
		}
		else if (a[i] < a[j])
		{
			res += (hight - j + 1) * a[i];  //已经排好序，那么右边一直到P2的位置都大于p1位置的数。			
			b[k++] = a[i++];   //按从小到大存放在 b 数组里面
		}
		else
		{
			b[k++] = a[j++];
		}
	}
	while (i <= mid)  // j 序列结束，将剩余的 i 序列补充在 b 数组中 
	{
		b[k++] = a[i++];
	}
	while (j <= hight)// i 序列结束，将剩余的 j 序列补充在 b 数组中 
	{
		b[k++] = a[j++];
	}
	k = 0;  //从小标为 0 开始传送
	for (int i = low; i <= hight; i++)  //将 b 数组的值传递给数组 a
	{
		a[i] = b[k++];
	}
	delete[] b;     // 辅助数组用完后，将其的空间进行释放（销毁）
	return res;
}
int mergesort_min(int* a, int low, int hight) //归并排序
{
	if (low == hight)
	{
		return 0;
	}
	int mid = (low + hight) / 2;
	return	mergesort_min(a, low, mid) + mergesort_min(a, mid + 1, hight) + merge_min(a, low, mid, hight);
}
int main()
{
	int a[5] = { 1,3,2,6,4 };
	mergesort(a, 0, 5 - 1);
	for (int i = 0; i < 5; i++)
	{
		cout << a[i];
	}
	int ans= mergesort_min(a, 0, 5 - 1);
	cout << ans;
	int x;
	cin >> x;
	return 0;
}