java链表的实现-单向链表中的元素位置视为索引均索引的作用

一.概述

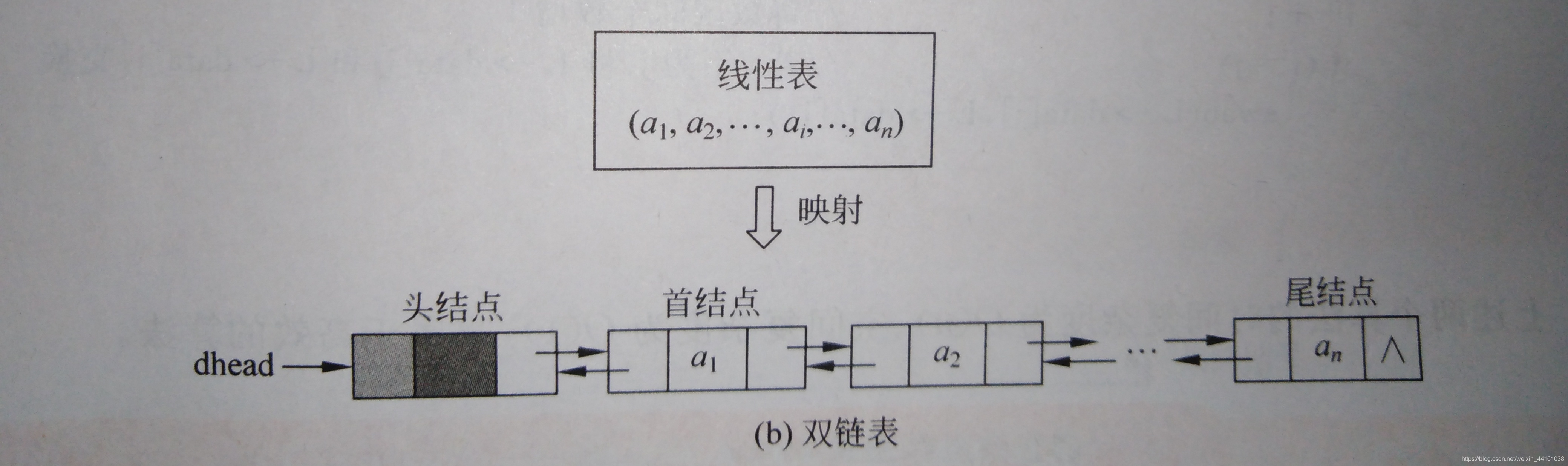
单向链表是链表的一种，它由多个结点组成，每个结点Node都由一个数据域和一个指针域组成java链表的实现，数据域用来存储数据， 指针域用来指向其后继结点，即保存后继结点的内存地址。

链表的头节点的数据域不存储数据，其指针域指向第一个真正存储数据的结点。

头节点的作用主要是用来找到当前这条链表。

二.链表的优缺点（和数组相反）

优点：随机增删元素效率较高，如果遇到随机增删集合中元素的业务比较多时，建议使用LinkedList（因为增删不涉及到大量元素位移）

缺点：查询效率较低，每一次查找某个元素的时候都需要从头节点开始往下遍历（链表的元素在的内存地址不连续，不能通过公式直接计算出元素的内存地址）

注意！！！

在顺序表中，由于数组是有索引的！在例如返回指定位置元素get(int i){}方法中，所传的参数 i 是指的索引。

而链表中是没有索引的！为了便于理解，故在此将链表中的元素位置（从0开始）视为索引，以下文中写的索引均为此意，并非是真的存在索引。

例如存入第一个元素“中国”，那么将这个元素的位置视为0，若要返回“中国”，则在get（）方法中的输入的参数 i=0 ，与顺序表的使用相同。

三.插入与删除原理

（1）插入元素

前提：链表是不存在索引的，此处将元素所在位置（从0开始）视为索引。

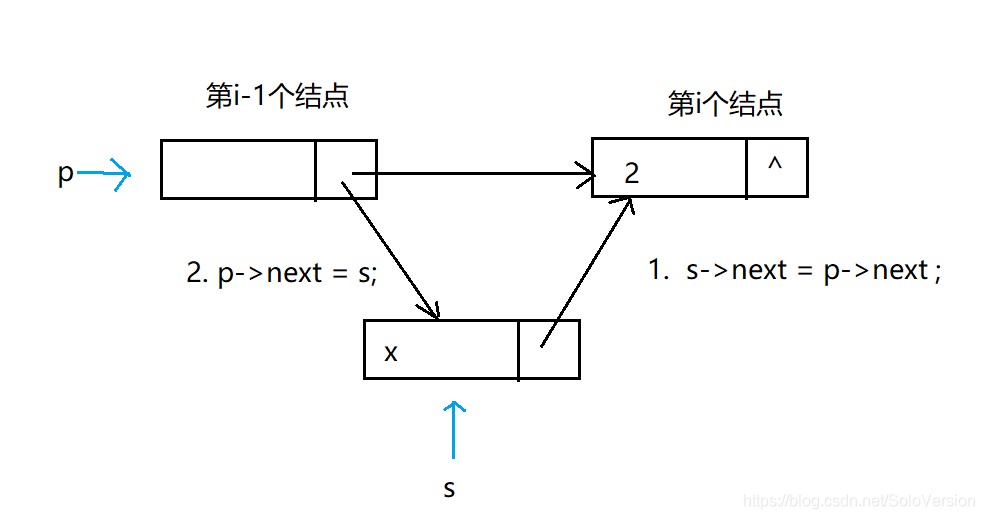
当在 “索引”i 位置插入新的结点时：

①找到并记录原来 i 位置的结点和前一个结点pre；

②将新结点newNode的指针域指向原 i 结点；（此时pre和newNode的指针域都保存有原i位置元素的内存地址）

③然后将原来 i 位置前面的元素pre的指针域指向新元素newNode即可。（pre的指针域由指向原i位置元素 变成了指向newNode，即pre和原 i 位置元素的连接断掉。）

注意：此处②③顺序不可变，必须先将newNode的指针域指向原 i 结点，再将pre的指针域指向newNode。假设一下，如果先将pre的指针域指向newNode，pre的指针域不再保存原 i 位置元素的内存地址，那么原来 i 元素及其后面的所有结点都会丢失，最终被 gc回收。

（2）删除元素

删除元素时，只需要将“索引” i 位置前面的元素pre连接到i位置后面的元素behind即可，具体步骤：

①找到并记录要删除的原 i 位置的结点和前一个结点pre（即位置为 i-1）；

②记录原 i 位置后面的结点behind；

③使pre结点的指针域指向behind

四.代码实现

首先创造一个LinkedList链表类，为了能够遍历，需要实现Iterable接口。

链表类的成员变量有：头节点head和记录结点个数的N，并在链表类的构造函数中初始化以上两个属性。

由于假设第一个元素的位置为0，所以不存数据的头节点的位置相当于是-1。

public class LinkedList <T> implements Iterable {
    private Node head; //头节点
    private int N;
    public LinkedList() {
        this.head = new Node(null, null); //头结点不存储数据
        this.N = 0;
    }

以内部类的方式创建结点类，结点类的成员变量有数据域data和指针域next：

 private class Node { //节点类 （成员内部类）
        T data;  //数据域
        Node next;  //指针域
        public Node(T data, Node next) {
            this.data = data;
            this.next = next;
        }
    }

清空链表，只需要让头节点的指针域为null，后面的所有结点都会被gc回收：

 public void clear() {
        head.next = null;  //断掉头节点与后面节点的连接即可清空，gc会将后面的节点清空
        this.N = 0;
    }

返回链表长度：

    public int length() {
         return N;
    }

是否为空：

    public boolean isEmpty() {
        return N == 0;
    }

由指定位置 i 返回一个结点的数据java链表的实现，先记录头节点，头节点视为"索引"为-1，第一个元素位置视为"索引"为0，而此处要返回的是"索引"为 i 的结点，即需要遍历 i +1次。

public T get(int i) { // i是假设的“索引”
        Node n = head; //记录头节点，相当于"索引"为-1
        for (int time = 0; time <i+1; time++) { //循环i+1次得到"索引"为 i 的节点
            n = n.next;
        }
        return n.data; //返回"索引"为 i 结点的数据
    }

向链表末尾添加元素：

 public void add(T t) {//只需要让目前最后一个节点的指针域指向一个新的节点
//首先找到当前最后的节点
        Node n = head; //记录头节点
        while (n.next != null) { //n.next为null即为最后一个节点
            n = n.next;
        }
//创造新节点(新的尾节点)，保存数据t
        Node newNode = new Node(t, null);
//让当前节点指向新节点
        n.next = newNode;
//元素个数+1
        this.N++;
    }

向指定"索引"添加元素，

这里先记录"索引"为 i 结点的前一个结点pre，那么pre的"索引"即为i-1，即需要迭代 i 次即得到pre。

  public void insert(T t,int i) {
//找到"索引"为i的前一个结点pre
        Node pre = head; //记录头节点，相当于是"索引"为-1
        for (int time = 0; time <i; time++) {  //共循环i次，得到"索引"为i-1的pre
            pre = pre.next;
        }
//找到"索引"为i的结点current
        Node current = pre.next;
//创建新节点，新节点newNode指向原i位置的节点current
//如果先将前节点连接新节点，则前节点的pre.next将改变，原i位置节点就会被新节点替换，后面的节点就连不上了，会被gc清除。
        Node newNode = new Node(t, current);  //此时pre和newNode的指针域都指向i位置节点current
//将pre指向新节点
        pre.next = newNode; //将pre的指针域从指向current变成指向newNode
//元素个数+1
        N++;
    }

根据指定位置删除元素：，i为假设的索引

先记录要删除的元素的前结点pre，其“索引”为i-1。

由 pre得到 i位置元素current。

由current得到 i位置后面的元素behind，

让pre指向behind即可。

 public T remove(int i) {
//找到“索引”为i-1的pre，遍历i次即可
        Node pre = head;//记录头节点，相当于“索引”为-1
        for (int time = 0; time <i; time++) {//循环i次，得到“索引”为i-1的前节点pre
            pre = pre.next; 
        }	
//找到i位置的节点
        Node current = pre.next;
//找到i位置的下一个节点
        Node behind = current.next;
//让i的前节点指向i的后节点
        pre.next = behind;
//元素个数-1
        N--;
        return current.data;
    }

查找出数据域t在链表中第一次出现的“索引”：

此处返回的 i 同样是假设的索引。

for循环的 i 正好对应“索引”大小

//链表的查询效率较低，每一次查找某个元素的时候都需要从头节点开始往下遍历
    public int indexOf(T t) {
//从头节点开始，依次找出每一个节点，求出data数据域，与t作比较
        Node n = head;
        for (int i = 0; n.next != null; i++) {  //链表无索引，使用for循环来计数
            n = n.next;
            if (n.data.equals(t)) {
                return i;  
            }
        }
        return -1;
    }

链表的遍历：

public Iterator iterator(){
        return new MyIterator(); 
    }
    private class MyIterator implements  Iterator{
        private Node n ; //记录每次迭代时拿到的当前结点
        
        public MyIterator(){
            this.n=head; //初始化当前结点
        }
        
        @Override
        public boolean hasNext() {
            return (n.next!=null);//判别当前节点是否还有元素可以遍历
        }
        @Override
        public Object next() { //返回迭代的下一个元素
            n=n.next;
            return n.data;
        }
    }

=========================================================================================================

完整代码及main测试

public class LinkedList <T> implements Iterable {
    private Node head; //头节点
    private int N;
    public LinkedList() {
        this.head = new Node(null, null); //建立头节点
        this.N = 0;
    }
    private class Node { //节点类 （成员内部类）
        T data;  //数据域
        Node next;  //指针域
        public Node(T data, Node next) {
            this.data = data;
            this.next = next;
        }
    }
    public void clear() {
        head.next = null;  //断掉头节点与后面节点的连接即可清空，gc会将后面的节点清空
        this.N = 0;
    }
    public int length() {
        return N;
    }
    public boolean isEmpty() {
        return N == 0;
    }
    public T get(int i) { // i是假设的“索引”
        Node n = head; //记录头节点，相当于索引为-1
        for (int time = 0; time <i+1; time++) { //循环i+1次得到"索引"为 i 的节点
            n = n.next;
        }
        return n.data; //返回"索引"为 i 结点的数据
    }
    public void add(T t) {//只需要让目前最后一个节点的指针域指向一个新的节点
//首先找到当前最后的节点
        Node n = head; //记录头节点
        while (n.next != null) { //n.next为null即为最后一个节点
            n = n.next;
        }
//创造新节点(新的尾节点)，保存数据t
        Node newNode = new Node(t, null);
//让当前节点指向新节点
        n.next = newNode;
//元素个数+1
        this.N++;
    }
    public void insert(T t,int i) {
//找到"索引"为i的前一个结点pre
        Node pre = head; //记录头节点，相当于是"索引"为-1
        for (int time = 0; time <i; time++) {  //共循环i次，得到"索引"为i-1的pre
            pre = pre.next;
        }
//找到"索引"为i的结点current
        Node current = pre.next;
//创建新节点，新节点newNode指向原i位置的节点current
//如果先将前节点连接新节点，则前节点的pre.next将改变，原i位置节点就会被新节点替换，后面的节点就连不上了，会被gc清除。
        Node newNode = new Node(t, current);  //此时pre和newNode的指针域都指向i位置节点current
//将pre指向新节点
        pre.next = newNode; //将pre的指针域从指向current变成指向newNode
//元素个数+1
        N++;
    }
    public T remove(int i) {
//找到“索引”为i-1的pre，遍历i次即可
        Node pre = head;//头结点，相当于位于0位置
        for (int time = 0; time <i; time++) {
            pre = pre.next; //循环i次，得到“索引 ”为i-1的pre
        }
//找到i位置的节点
        Node current = pre.next;
//找到i位置的下一个节点
        Node behind = current.next;
//让i的前节点指向i的后节点
        pre.next = behind;
//元素个数-1
        N--;
        return current.data;
    }
//链表的查询效率较低，每一次查找某个元素的时候都需要从头节点开始往下遍历
    public int indexOf(T t) {
//从头节点开始，依次找出每一个节点，求出data数据域，与t作比较
        Node n = head;
        for (int i = 0; n.next != null; i++) {  //链表无索引，使用for循环来计数
            n = n.next;
            if (n.data.equals(t)) {
                return i;
            }
        }
        return -1;
    }
    public Iterator iterator(){
        return new MyIterator();
    }
    private class MyIterator implements  Iterator{//成员内部类
        private Node n ;
        public MyIterator(){
            this.n=head; //即从头节点开始
        }
        @Override
        public boolean hasNext() {
            return (n.next!=null);//判别当前节点是否还有元素可以遍历
        }
        @Override
        public Object next() { //返回迭代的下一个元素
            n=n.next;
            return n.data;
        }
    }
    public static void main(String[] args) {
        LinkedList<String> list=new LinkedList<>();
        System.out.println("-------");
        list.add("中国");
        list.add("美国");
        list.add("俄罗斯");
        list.add("法国");
        System.out.println(list.length());//输出： 4
        for (Object data : list) {
            System.out.println(data);
        }//输出：中国  美国 俄罗斯  法国
        System.out.println("---------");
        list.insert("加拿大",2);
        System.out.println(list.indexOf("加拿大"));//输出：2
        System.out.println(list.get(2));//输出：加拿大
        System.out.println("----------------");
        System.out.println(list.length());//输出： 5
    }
}

注意：

链表无索引，此处为了理解，将元素位置假设为索引，和索引一样从0开始头结点“索引”为-1，第一个元素“索引”为0，最后一个元素索引为 i-1要得到索引为 i 的元素，要遍历 i+1 次

五.复杂度分析

get(int i)：每一次查询，都需要从链表的头部开始，依次向后查找时间复杂度为O(n)

insert(int i,T t)：每一次插入，需要先找到i位置的前一个元素，然后完成插入操作，时间复杂度为O(n);

remove(int i）：:每一次移除，需要先找到i位置的前一个元素，然后完成插入，时间复杂度为O(n)

相比较顺序表，链表插入和删除的时间复杂度虽然一样，但仍然有很大的优势，因为链表的物理地址是不连续的，它不需要预先指定存储空间大小，或者在存储过程中涉及到扩容等操作； 同时O（n）只是耗在了for循环遍历。它并没有涉及的元素的交换。

相比较顺序表，链表的查询操作性能会比较低。

因此，如果查询操作比较多，建议使用顺序表，增删操作比较多，建议使用链表。