递归算法解决因式分解java版-分解三次因式公式

第2章递归第页⒈教学内容递归的概念递归调用的实现原理递归转换为非递归汉诺塔问题⒉教学目的理解递归的特点会分析定性数据统计分析pdf销售业绩分析模板建筑结构震害分析销售进度分析表京东商城竞争战略分析什么样的问题适合用递归解决领会递归调用的执行过程了解递归的优点了解递归的缺点⒊教学重点什么样的问题可以用递归解决递归实现的方法快递客服问题件处理详细方法计算方法pdf计算方法pdf山木方法pdf华与华方法下载递归方法的时空效率⒋教学难点递归的执行过程递归转换为非递归第页例1一个人要搬走10块石头怎么搬呢例2计算从1到100的累加和例3计算2n这些定义方式体现了一种逻辑思想同时又是一种解决问题的方案气瓶 现场处置方案递归算法解决因式分解java版.pdf气瓶 现场处置方案 .doc见习基地管理方案递归算法解决因式分解java版.doc关于群访事件的化解方案建筑工地扬尘治理专项方案下载递归定义的问题可以用递归的算法来求解21引言1问题的提出第页2递归的概念递归是一个过程或函数直接或间接调用自身的一种方法它可以把一个大型的问题层层转化为一个与原问题相似但规模较小的问题来求解数学中阶乘的定义n的阶乘可以如下表关于同志近三年现实表现材料材料类招标技术评分表图表与交易pdf视力表打印pdf用图表说话 pdf示再如斐波那契Fibonacci数列指的是这样一个数列直接或间接调用自身的程序称为递归程序递归是一种特殊的嵌套调用是某个函数调用自己而不是另外一个函数这是一种函数直接或者间接调用自身编程技术第页22递归调用的实现原理1递归算

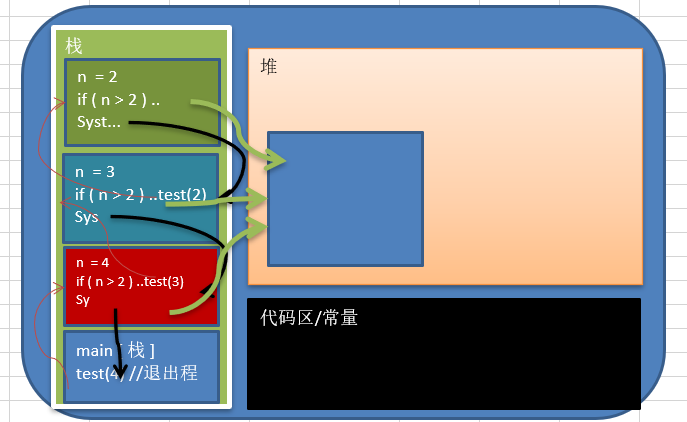
法的构成能够用递归解决的问题应该满足以下三个条件需要解决的问题可以化为一个或多个子问题来求解而这些子问题的求解方法与原来的问题完全相同只是在数量规模上不同递归调用的次数必须是有限的必须有结束递归的条件边界条件来终止递归第页递归算法的设计一般分为两步第一步将规模较大的原问题分解为一个或多个规模较小的而又类似于原问题特性的子问题既将较大的问题递归地用较小的子问题来描述解原问题的方法同样可以用来解决子问题第二步是确定一个或多个不需要分解可直接求解的最小子问题第页第页2递归调用的内部过程算法2-1中求阶乘的问题假设程序运行时n＝4那么程序的执行过程第页从上面可以看出递归调用的过程分为两个阶段1递归过程将原始问题不断转化为规模小了一级的新问题从求4变成求3变成求2最终达到递归终结条件求12回溯过程从已知条件出发沿递归的逆过程逐一求值返回直至递归初始处完成递归调用第页2递归调用的内部过程在这两个阶段中系统会分别完成一系列的操作在递归调用之前系统需完成三件事为被调用过程的局部

变量分配存储区将所有的实参返回地址等信息传递给被调用过程保存将控制转移到被调过程的入口从被调用过程返回调用过程之前系统也应完成三件工作保存被调过程的计算结果释放被调过程的数据区依照被调过程保存的返回地址将控制转移到调用过程在计算机中是通过使用系统栈后面的章节会介绍ldquo栈rdquo来完成上述操作的第页递归算法解决问题的方式和特点是将初始问题可转化为解决方法相同的新问题而新问题的规模要比原始问题小新问题又可以转化为规模更小的问题helliphellip直至最终归结到最基本的情况mdashmdash递归的终结条件递归方法有许多不利之处递归调用会占用大量的内存和消耗大量的时间造成执行效率低但有时采用递归方法编写的程序简洁清晰可读性好第页23递归转换为非递归1递归转化为递推当递归算法所涉及的数据定义形式是递归的情况下通常可以将递归算法转化为递推算法用递归的边界条件作为递推的边界条件比如求阶乘斐波那契数列等递推也是一种从已知条件出发用一种具体的算法一步一步接近未知一

般采用循环结构经常和枚举配合使用递推算法在求解的过程中每一个中间量都是已知而且没有重复计算运算简洁但是书关于书的成语关于读书的排比句社区图书漂流公约怎么写关于读书的小报汉书pdf写代码和理解代码比较难第页第页递归是从未知到已知再从已知返回未知利用子问题与父问题的关系进而构造成有递归性的函数而递推是与此相反从已知到未知类似于一般解数学题的思路从未知与已知的顺序上来看他们好像是逆过程但我认为不是递归把问题简单化抓的是问题与子问题的联系而递推是把中间解推进抓得是中间量与更靠近未知的中间量的联系两者不同不能看成逆过程第页2递归转化为回溯对于可以用回溯算法解决的问题也可以用非递归的回溯来实现如在本章ldquo实验题rdquo中的八皇后问题回溯方法的步骤如下定义一个解空间它包含问题的解用适于搜索的方式组织该空间用深度优先法搜索该空间利用限界函数避免移动到不可能产生解的子空间第页3手工模拟递推设P是一个递归算法假定P中共有m个值参和局部变量共有t处递归调用P的语句则把P改写成一个非递归算法的一般规则为１定义一个栈S用来保存每次递归调用前值参和局部变

量的当前值以及调用后的返回地址即S应该含有m1个域且S的深度必须足够大使得递归过程中不会发生栈溢出２定义t2个语句标号其中用一个标号标在原算法中的第一条语句上用另一个标号标在作返回处理的第一条语句上其余t个标号标在t处递归调用的返回地址分别标在相应的语句上第页３把每一个递归调用语句改写成如下形式把值参和局部变量的当前值以及调用后的返回地址压入栈把值参所对应的实际参数表达式的值赋给值参变量无条件转向原算法的第一条语句4在算法结束前增加返回处理当栈非空时做出栈把原栈顶中前m个域的值分别赋给各对应的值参和局部变量无条件转向由本次返回地址所指定的位置第页5增设一个同S栈的成分类型元素相同的变量作为进出栈的缓冲变量对于递归函数还需要再增设一个保存函数值中间结果的临时变量用这个变量替换函数体中的所有函数名待函数结束之前在把这个变量的值赋给函数名返回6在原算法的第一条语句之前增加一条把栈置空的语句7对于递归函数而言若某条赋值语句中包含两处或多处递归调用假设为n处则应首先把它拆

成n条赋值语句使得每条赋值语句只包含一处递归调用同时对增加的n-1条赋值语句要增设n-1个局部变量然后按以上六条规则转换成非递归函数第页24典型题分析－汉诺塔问题1汉诺塔问题描述有abc三个底座底座上面可以放盘子初始时a座上有n个盘子这些盘子大小各不相同大盘子在下小盘子在上依次排列要求将a座上n个盘子移至c座上每次只能移动一个并要求移动过程中保持小盘子在上大盘子在下可借助b座实现移动编程序输出移动步骤第页2汉诺塔问题分析这个问题可用递归思想来分析将n个盘子由a座移动到c座可分为如下三个过程先将a座上n-1个盘子借助c座移至b座再将a座上最下面一个盘子移至c座最后将b上n-1个盘子借助a移至c座上述过程是把移动n个盘子的问题转化为移动n-1个盘子的问题按这种思路再将移动n-1个盘子的问题转化为移动n-2个盘子的问题helliphellip直至移动一个盘子可以用两个函数来描述上述移动过程从一个底座上移动n个盘子到另一底座从一个底座上移动1个盘子到另一底座第页